Mathématiques I
Le problème posé avait pour thème les fonctions absolument monotones. La partie I fournissait des exemples de telles fonctions obtenues soit à partir de fonctions élémentaires, soit à partir de transformées de Laplace de mesures positives. La partie II, étudiait l'analycité des fonctions absolument monotones. Quant à la partie III, elle fournissait un nouvel exemple de fonctions absolument monotones à savoir les fonctions totalement monotones.
Le problème était long et demandait a priori un certain savoir faire. Le sujet quelque peu innovant dans les questions I.F balayait une large partie du programme d'analyse des deux années de préparation. Pratiquement aucun candidat ne l'a traité complètement et de nombreuses copies ne se contentent que de survoler les parties I et II. De façon détaillée, voici les remarques que l'on peut formuler.
Partie I
A. Tout d'abord quelques candidats ne connaissent pas la formule de Leibniz à l'ordre n. D'autre part, un quart des candidats ne sait pas répondre à la question ouverte portant sur le produit de deux fonctions complètement monotones.
B.
Le taux de réussite est de l'ordre de 30%. L'échec peut s'expliquer par le fait qu'on ne sait pas exploiter l'indication du texte qui demandait à raisonner par récurrence donc à écrire que 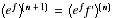 . Les candidats qui ne suivent pas cette recommandation se divisent en deux catégories : ceux qui essaient d'écrire de façon explicite la dérivée nième de
. Les candidats qui ne suivent pas cette recommandation se divisent en deux catégories : ceux qui essaient d'écrire de façon explicite la dérivée nième de 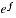 et ceux qui pensent que la notion d'absolue monotonie est stable par passage à la limite simple et qui écrivent
et ceux qui pensent que la notion d'absolue monotonie est stable par passage à la limite simple et qui écrivent
C. Cette question est vue mais très mal rédigée de façon générale.
D.1.
La vérification est généralement faite mais de très nombreux candidats oublient de constater que la fonction est à valeur positive. On peut noter aussi qu'un pourcentage non négligeable de candidats ne sait pas calculer les dérivées successives de la fonction 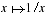 .
.
D.2.
Cette question est très sélective : 20% des candidats l'établissent ; 40% proposent une méthode qui aurait pu aboutir mais qu'ils sont incapables de mener à bien ; 20% proposent une démarche erronée reposant sur des expressions fantaisistes, des dérivées successives de la fonction 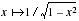 ; 20% ne l'abordent pas.
; 20% ne l'abordent pas.
Il convient par ailleurs de signaler que parmi les candidats qui utilisent le développement en série entière de 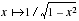 un grand nombre calcule les dérivées successives par dérivation terme à terme sans référence à tout énoncé.
un grand nombre calcule les dérivées successives par dérivation terme à terme sans référence à tout énoncé.
D.4.
Dans de très nombreuses copies, on observe que 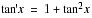 puis on affirme sans la moindre preuve, que la dérivée nièmè de la fonction
puis on affirme sans la moindre preuve, que la dérivée nièmè de la fonction 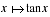 est un polynôme à coefficients positifs en
est un polynôme à coefficients positifs en 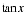 . Du coup le rendement est de l'ordre de 50%.
. Du coup le rendement est de l'ordre de 50%.
E.1.
et
2.
Ces questions -- qui à vrai dire ne sont que "des questions de cours" -- n'ont permis qu'à un très petit nombre de candidats de marquer des points. En effet 50% des candidats croient qu'en un point, une fonction réelle admet toujours une limite dans 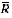 et 25% affirment que la continuité sur
et 25% affirment que la continuité sur 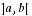 garantit l'existence d'une limite au point a. Un constat s'impose : le théorème de la limite monotone et le théorème de prolongement des fonctions de classe
garantit l'existence d'une limite au point a. Un constat s'impose : le théorème de la limite monotone et le théorème de prolongement des fonctions de classe 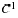 ne sont pas connus ou lorsqu'ils le sont, sont mal exploités.
ne sont pas connus ou lorsqu'ils le sont, sont mal exploités.
F.1 La question est traitée correctement par 60% des candidats. Les autres proposent des solutions basées sur le fait que toute fonction réelle est soit positive, soit négative, soit dans le cas le plus défavorable de signe constant par morceaux.
F.2. Cette question facile a priori s'avère un piège redoutable pour 30% des copies.
F.3.
Cette question n'est traitée entièrement de façon correcte que par 5% des candidats. Cela peut s'expliquer par le fait que l'on confond une fonction et la valeur que prend cette fonction en un point : la manipulation de la fonction 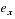 est très éclairante à ce sujet. Sans se soucier du statut de la fonction
est très éclairante à ce sujet. Sans se soucier du statut de la fonction 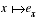 , on affirme que cette fonction est continue car la fonction exponentielle l'est et on déduit la continuité de
, on affirme que cette fonction est continue car la fonction exponentielle l'est et on déduit la continuité de 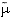 en composant par la forme
en composant par la forme 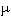 qui est continue car linéaire. On peut noter aussi que 10% des candidats établissent la décroissance de la fonction
qui est continue car linéaire. On peut noter aussi que 10% des candidats établissent la décroissance de la fonction 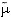 en montrant (de façon délictueuse) que cette fonction est dérivable et de dérivée négative ; ayant oublié qu'une fonction dérivable est nécessairement continue, ces mêmes candidats démontrent (de façon toute aussi délictueuse) la continuité de
en montrant (de façon délictueuse) que cette fonction est dérivable et de dérivée négative ; ayant oublié qu'une fonction dérivable est nécessairement continue, ces mêmes candidats démontrent (de façon toute aussi délictueuse) la continuité de 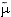 .
.
F.4. Le taux de réussite est analogue à celui de 3. Il convient de souligner que le texte fournissait une indication rarement utilisée ou totalement ignorée.
F.5.
Dans de très nombreuses copies, on ne sait pas exploiter 4 et on recommence pour la troisième fois un raisonnement erroné reposant sur la linéarité de la forme 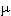 .
.
Partie II
A.1.
Deux tiers des candidats ne connaissent pas la formule de Taylor avec reste intégral. Parmi ceux qui la connaissent, 80% gardent le reste sous forme d'une intégrale sur le segment 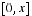 et appliquent à cette intégrale des résultats valides pour des intégrales attachées à un intervalle fixe de telle sorte que le taux de réussite à cette question est très faible.
et appliquent à cette intégrale des résultats valides pour des intégrales attachées à un intervalle fixe de telle sorte que le taux de réussite à cette question est très faible.
A.2. Cette question n'est réussie que par 20% des candidats. La majorité des candidats invoque la règle de d'Alembert et ne parvient pas à établir la majoration demandée.
A.3.
Cette question est globalement vue mis à part le problème posé par 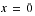 qu'il faut traiter à part.
qu'il faut traiter à part.
A.4. Le taux de rendement est de l'ordre de 2%. Ici encore beaucoup de candidats ignorent l'indication fournie par le texte.
B. Rares sont les candidats qui effectuent une translation pour ramener cette question à ce qui précède.
C.
Si, de façon maladroite parfois, la première partie de cette question est effectuée par l'ensemble des candidats l'ayant abordée, seul un petit nombre d'entre eux a été capable de caractériser les fonctions absolument monotones dont une dérivée s'annule dans 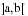 .
.
Partie III
A. Cette question élémentaire n'est traitée correctement que par 5% des candidats.
B. La majorité des candidats résolvent cette question à l'aide d'un raisonnement par récurrence dont l'hypothèse n'est jamais écrite de façon correcte.
C. Le calcul demandé est effectué mais, de façon générale, on ne sait pas l'exploiter pour conclure.
D. La première question est réussie par ceux qui l'abordent. À part quelques rares exceptions, les questions 2 et 3 ne sont pas traitées de façon significative.
Conclusion
Ce problème a montré que peu de candidats maîtrisent correctement les notions intervenant dans cet énoncé. Les copies excellentes sont rares, par contre le nombre de copies quasiment vides est important. Pour améliorer cette situation, on recommande aux futurs candidats de connaître les énoncés fondamentaux du cours, de savoir justifier avec concision les variations qu'ils présentent, de lire attentivement l'énoncé proposé et de ne pas ignorer les indications fournies par le texte.
 .
.
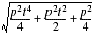 ,
,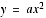 .
.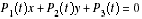 a souvent été comprise comme une relation linéaire entre les Pi, et, de ce fait, la réponse a été parfois aberrante "les droites Dt doivent être vides", ou le plus souvent absente, chez les candidats s'étant rendu compte de l'absurdité du résultat. C'est un principe analogue qui a fait passer, en
I.B.2b
,
c
,
d
de "(x, y) est unique" à "t est unique"... d'où la nullité du discriminant.
a souvent été comprise comme une relation linéaire entre les Pi, et, de ce fait, la réponse a été parfois aberrante "les droites Dt doivent être vides", ou le plus souvent absente, chez les candidats s'étant rendu compte de l'absurdité du résultat. C'est un principe analogue qui a fait passer, en
I.B.2b
,
c
,
d
de "(x, y) est unique" à "t est unique"... d'où la nullité du discriminant.