Mathématiques I
Le problème proposé aux candidats de la filière PSI était celui de la courbe dite "brachistochrone". Ce problème s'énonce de la façon suivante :
"Étant donnés deux points A et B dans un même plan vertical, trouver une courbe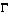 
joignant A à B telle que le temps mis par un mobile ponctuel soumis à l'accélération de la pesanteur et se déplaçant sans frottement sur 
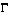pour aller de A en B soit le plus court possible".
On trouve évidemment que cette courbe est un segment de droite si A est à la verticale de B ; le résultat général est que la courbe brachistochrone est une demi-arche de cycloïde.
Ce problème est d'une grande importance historique, car il a motivé des travaux d'Euler puis de Lagrange qui ont donné naissance à une branche des Mathématiques appelée "Calcul des variations" et à la formulation moderne de toutes les lois élémentaires de la Physique.
L'énoncé était formé de trois parties d'importances inégales.
Dans la partie I, on faisait découvrir aux candidats certaines propriétés géométriques des arches de cycloïdes. Il n'y avait pas de réelle difficulté, sauf sur la question I.C où les candidats ont presque toujours peiné sur la façon d'orienter les arches de cycloïdes proposées dans l'énoncé. La question I.E préparait le lien entre les calculs analytiques de la partie II et la description géométrique de la partie I. La seule difficulté était la singularité en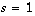 
qui n'apparaissait que pour 
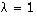. En dominant l'intégrande par 
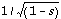, on réglait la question d'intégrabilité du I.E.1 et la continuité du I.E.2 par convergence dominée. Les bons candidats se sont en général fort bien acquittés de cette tâche. Les questions I.E.3 et 4 ne posaient aucune difficulté particulière et faisaient établir le lien entre l'arche de cycloïde (C) et le graphe d'une primitive de 
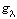, le but de la partie II étant de démontrer par une méthode analytique que la brachistochrone est donnée comme le graphe de la primitive de 
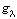s'annulant en 0.
Cette première partie faisait appréhender concrètement la solution du problème de minimisation posé au II et habituait les candidats à certains objets ou formules apparaissant dans la suite. Elle a été généralement bien traitée par les candidats ayant travaillé sérieusement le programme.
La partie II était le coeur du problème. Encore faut-il observer que, par rapport au calcul classique permettant d'aboutir à l'équation d'Euler pour une courbe extrémale, la voie proposée dans l'énoncé évitait une difficulté en faisant travailler avec la dérivée de la solution (ce qui évite une intégration par parties pour exprimer la variation sur les dérivées de la fonction inconnue en termes de la variation sur la fonction inconnue elle-même). Les autres difficultés du calcul des variations subsistaient (argument de dualité basé sur l'utilisation de fonctions tests, vérification de la minimalité etc.). C'est dire que cette partie était de nature très conceptuelle pour des candidats ne se spécialisant pas en Mathématiques.
La quasi-totalité des copies s'arrêtaient au II.D.1, sauf pour traiter quelques questions très simples éparpillées dans la fin du problème. Le II.A a mis beaucoup de candidats en difficultés : il fallait bien maîtriser la notion de borne inférieure (savoir qu'une partie non vide minorée de
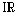possède une borne inférieure, savoir que tout minorant de cette partie minore sa borne inférieure, etc.). Ces notions sont fort délicates à manipuler, ceci confirme l'impression dégagée par le même problème pour la session précédente (1997) portant sur les séries de Dirichlet. Les candidats dominant bien ces notions n'ont eu aucun mal à encadrer m(a) et à trouver la limite demandée au II.B.
Le II.C.1 demandait de savoir appliquer le théorème de dérivation sous le signe somme. Le calcul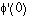 
au II.C.2 était une application directe de l'expression de la dérivée de 
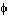obtenue au II.C.1 (on pouvait bien sûr écrire la formule sans justification, celle-ci faisant l'objet de la question II.C.1). Pour la deuxième partie de la question, il fallait se souvenir de l'énoncé sur les formes linéaires rappelé dans les premières lignes de l'énoncé. Cela a gêné beaucoup moins de candidats qu'on aurait pu le craindre (sans doute l'énoncé rappelé était familier à un grand nombre d'entre eux). Il s'agissait d'une question a priori délicate où les candidats se sont en moyenne bien comportés. Le II.C.3 était encore une question délicate : il était souhaitable de dessiner le graphe de 
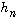afin d'avoir l'intuition du mécanisme de la preuve. Beaucoup de candidats ont eu ce réflexe ; certains ont même remarqué le phénomène de concentration en 
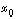qui est la clef du résultat : cela était déjà fort satisfaisant. Très peu de copies arrivent à une démonstration sans l'aide de la représentation graphique. Le II.C.4 était une application directe du II.C.3, mais il fallait encore faire attention aux inégalités demandées sur 
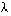: c'est finalement ce point particulier sur lequel la grande majorité a achoppé. Le II.C.5 demandait de se souvenir des résultats du I.E.
Comme nous l'avons dit, presqu'aucun candidat n'a obtenu de résultat satisfaisant sur la suite du problème (par exemple, nous avons relevé plusieurs tentatives malheureuses de résolution du II.D.2 par une double dérivation sous le signe somme alors qu'il aurait suffi d'observer que la fonction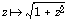 
est convexe). Mais l'énoncé proposé était copieux et, par endroits, difficile de sorte que les questions I.A à II.C.5 suffisaient à départager très sérieusement les candidats. De plus, l'énoncé permettait de jauger les capacités des candidats sur de nombreux points du programme (géométrie des courbes, convergence d'intégrales, intégrales à paramètres, théorème de convergence dominée, théorème de dérivation sous le signe somme, notion de borne inférieure) qui en constituent le noyau dur.
Enfin, le jury a apprécié le fait que la plupart des copies étaient plutôt bien rédigées. Sans doute cela est-il dû au fait que le problème était posé de façon ouverte -- c'est-à-dire sous forme de questions formulées sans réponse plutôt que sous forme d'une suite de propositions intermédiaires à démontrer. De tels énoncés incitent les candidats à une réflexion plus poussée (d'abord en les obligeant à deviner ce qu'ils doivent démontrer) et à se servir des résultats qu'ils ont eux-mêmes découverts pour avancer dans le problème : c'est sans doute la raison des progrès dans la qualité de la rédaction des copies par comparaison avec celles de l'an dernier. Le jury encourage vivement les candidats à poursuivre dans cette voie.
qu'il était à l'initiative du candidat de mener. Ceux qui répondent sèchement "oui" ou "non" aux questions I.A.3 et I.A.4 n'obtiennent aucun point, même si la réponse est juste ! Comme la réponse était "non" dans les deux cas, la meilleure justification était un contre exemple, assorti d'une explication.
, "cela convient".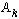
, ce qui permet de régler les affectations en une boucle). Une minorité de candidats traitent correctement ces questions, qui rapportent pourtant beaucoup de points.
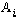et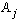 
pour i différent de j, le mieux était une double boucle, la boucle sur j partant de i + 1. La variable OK devait être initialisée à 1. Il était inutile d'utiliser des compteurs.
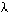est strictement inférieur à 1, la suite 
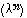tend vers 0, mais on ne peut rien dire en cas d'inégalité large en général. Beaucoup de candidats traitent correctement III.A.3.a et b ; la difficulté du c, vient du fait qu'il faut diviser par la somme des composantes de V et donc s'assurer que celle-ci est non nulle. En III.B.1 les résultats approximatifs n'ont pas été acceptés, la forme de la matrice 
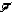composée de deux blocs identités devait être clairement donnée. Ensuite, les candidats astucieux pouvaient se rendre compte que l'essentiel des questions 1.c et 1.d avait été résolu précédemment. La majorité des candidats qui abordent la question 1.c se trompent dans l'expression du produit scalaire de 
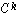, oubliant qu'il faut conjuguer les coordonnées du premier vecteur. Le III.B.2 se traitait de la même façon que le III.A.1 : il fallait donc contrôler le module des valeurs propres de la matrice.