Mathématiques I
Le niveau d'ensemble des candidats est satisfaisant. La bonne impression laissée par les candidats de la filière PSI de l'année dernière a été confirmée.
Il y a peu de candidats très faibles. La plupart connaissent bien les théorèmes du cours et savent les appliquer sur des exemples simples. Quelques très bons candidats ont réalisé de remarquables interrogations.
Remarques générales et conseils pour les futurs candidats
Le jury a été très sévère avec les quelques candidats qui donnent des énoncés approximatifs des théorèmes du cours d'analyse. Il est par exemple très difficile d'obtenir de la part de certains candidats toutes les hypothèses et les conclusions pour les théorèmes d'interversion des intégrales et des séries.
Les dépassements de programme sont toujours dangereux.
Que penser, par exemple, d'un candidat qui évoque à propos du théorème de Dirichlet des "pseudo-dérivées" à droite et à gauche mais qui est incapable de donner la définition d'une fonction de classe 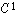 par morceaux ?
par morceaux ?
Les énoncés des théorèmes sont suffisamment détaillés dans le programme officiel.
Toute extrapolation est dangereuse car elle risque de ne pas être maîtrisée.
Le programme de cette épreuve de mathématiques I n'est pas "intégrales et séries" comme certains candidats semblent le croire mais "analyse et géométrie différentielle". Le jury a interrogé les candidats sur l'ensemble du programme.
Les résultats en géométrie différentielle sont souvent catastrophiques. Le programme est pourtant très réduit et devrait être maîtrisé. Les exercices proposés sont très simples mais peu de candidats sont capables d'étudier une courbe en coordonnées polaires et le calcul d'un rayon de courbure pose beaucoup de difficultés.
L'épreuve orale au tableau ne dure que trente minutes. Certains candidats, sans doute trop contents d'avoir trouvé une solution, prennent plaisir à l'exposer lentement de peur peut-être de se voir poser d'autres questions. Ce n'est évidemment pas la bonne méthode : l'exercice proposé n'est souvent qu'un tremplin, l'examinateur appréciant avant tout la vivacité et la pertinence des réparties au cours du dialogue qui suit l'exposé initial.
À l'inverse on peut très bien, même si la préparation de 30 minutes a semblé infructueuse, faire une bonne interrogation : la faculté qu'a un candidat à exploiter l'aide qu'on lui fournit est un élément important d'appréciation. Certains candidats attendent que l'examinateur acquiesce à chacune de leurs affirmations avant d'avancer. Les candidats doivent faire preuve de plus d'autonomie. Il est évident que l'examinateur ne les laissera pas durablement continuer dans une voie vouée à l'échec.
Erreurs les plus fréquemment rencontrées
Le jury a noté avec satisfaction que certaines erreurs signalées dans le rapport de l'année dernière ont presque disparu. Par exemple, la majorité des candidats vérifient bien que dans les théorèmes de convergence monotone et dominée la limite simple est bien continue par morceaux. De même peu de candidats continuent à penser que la convergence uniforme sur I de 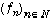 vers f suffit pour montrer que
vers f suffit pour montrer que 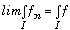 quand I est un intervalle quelconque.
quand I est un intervalle quelconque.
En revanche certains semblent avoir oublié le théorème de convergence uniforme quand I est un segment.
Beaucoup de candidats évoquent encore la notion d'intégrale convergente et font ensuite la confusion entre l'intégrabilité de f sur 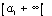 et l'existence de
et l'existence de
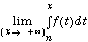
Le jury, conformément au programme, ne demande cependant aucune connaissance spécifique aux candidats sur les intégrales semi-convergentes.
La formule de Stirling n'est pas connue. Certains candidats affirment qu'elle n'est pas au programme.
Le jury a toujours droit à "la convergence normale d'une série entière sur l'intervalle ouvert de convergence".
Certains candidats continuent à ignorer la méthode de variation des constantes pour les équations différentielles linéaires du second ordre. Ils ont été sévèrement sanctionnés.
Les théorèmes d'existence et d'unicité pour les équations différentielles scalaires du 1er ordre 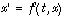 et pour les systèmes autonomes ne sont pas connus.
et pour les systèmes autonomes ne sont pas connus.
Pour vérifier la continuité d'une fonction de 2 variables réelles beaucoup de candidats se contentent d'établir la continuité des applications partielles.
Très peu de candidats savent que si une série trigonométrique converge uniformément sur R c'est la série de Fourier de sa somme.
Les candidats ne savent pas étudier les branches infinies d'une courbe en coordonnées polaires.
Mathématiques II
Le niveau moyen des candidats interrogés à cette épreuve reste à peu près constant.
Cette épreuve vise à tester les connaissances des candidats en algèbre et géométrie, leur capacité d'adaptation à une situation particulière, et leur maîtrise des techniques nécessaires à la résolution de la question. Avant de signaler les erreurs les plus fréquemment rencontrées, nous voudrions commenter trois aspects de l'interrogation :
-
Le candidat se présente au tableau après trente minutes de préparation au cours desquelles l'examinateur n'intervient pas. Il n'est pas attendu que l'exercice donné soit entièrement traité durant la demi-heure de préparation. En revanche, on attend des candidats qu'ils aient réfléchi à la situation proposée, qu'ils se soient familiarisés avec le problème, et qu'ils aient essayé plusieurs pistes, avec l'aide éventuelle de leur calculatrice ou du logiciel de calcul formel mis à leur disposition. Non seulement celui-ci peut les décharger de calculs longs et fastidieux, mais il peut aussi les aider à anticiper un résultat. Encore faut-il connaître quelques rudiments de syntaxe, notamment certaines commandes de la bibliothèque
linalg
, fort utiles dans l'étude des matrices. Citons par exemple
eigenvects
,
charpoly
ou
gaussjord
. Plus grave encore, certains étudiants ignorent encore la syntaxe du calcul matriciel, par exemple
&*
, ou
evalm
. Nous n'exigeons aucune érudition en la matière, et l'objet de l'épreuve ne consiste pas à évaluer les connaissances du candidat en calcul formel, mais n'est-il pas stupide de gaspiller 20 minutes du temps de préparation à faire (et souvent en commettant des erreurs) des calculs que le logiciel peut effectuer instantanément ? De fait, les candidats qui, pendant leurs années de préparation, ont suivi avec sérieux les séances d'interrogation ou de travaux dirigés destinés à l'apprentissage d'un logiciel de calcul formel se trouvent très avantagés dans cette épreuve.
-
Un test de connaissance peut prendre plusieurs formes : on peut demander au candidat de citer avec précision un théorème employé, de refaire la démonstration d'un résultat classique en rapport avec la question posée, ou encore d'analyser des résultats obtenus en les resituant dans une perspective plus large vis-à-vis du cours. Il est agréable de constater que de tels sondages sont en général positifs : la grande majorité des candidats connaissent le cours, même s'ils ne l'appliquent pas toujours correctement au niveau de la méthode.
-
La capacité du candidat à s'adapter à la question qui lui est posée constitue elle aussi un élément majeur de l'évaluation :
le jury attend du candidat une solution adaptée au problème posé, et non pas la reproduction à l'identique de la solution d'un autre problème qu'il a déjà traité ou vu traiter
. Les questions posées ou les suggestions de l'examinateur sont toujours progressives, et permettent donc une "montée en puissance". Celle-ci suppose évidemment un dialogue entre examinateur et candidat. Ce dialogue, qui joue lui aussi un rôle important dans l'évaluation, doit être pertinent, précis, efficace. Signalons à ce sujet que le jury refuse de communiquer par sigles, et qu'il rejette en bloc les "sin", "cos", "det", "seps" et autres "vaps" (traduisez "sous-espaces propres" et "valeurs propres"). De même, l'adjectif "inférieur" demande souvent à être préciser (strictement ou largement ?), et les valeurs absolues ne sont pas uniquement un élément de décor... Il n'est pas rare d'entendre que la suite
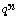 tend vers zéro, dès lors que
tend vers zéro, dès lors que 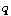 est inférieur à 1.
est inférieur à 1.
Signalons à présent quelques points particuliers sur lesquels trop de candidats révèlent de graves ignorances.
-
Les raisonnements par condition nécessaire et suffisante, ou par analyse et synthèse sont loin d'être dominés, alors qu'ils sont d'usage fréquent en algèbre linéaire (problèmes de sommes directes, de recherche de bases adaptées à un endomorphisme...).
-
La recherche de sous-espaces stables par un endomorphisme est un moyen souvent commode de réduction sans calcul du polynôme caractéristique. Rappelons par ailleurs que, lorsque f est un endomorphisme auto-adjoint, son image et son noyau sont supplémentaires orthogonaux, et sont tous deux stables par f.
-
Les notions de matrices équivalentes et de matrices semblables sont trop souvent confondues.
-
La classification des isométries vectorielles en dimension 3 est méconnue, et trop de candidats persistent à croire qu'une projection orthogonale est un automorphisme orthogonal.
-
La définition du produit vectoriel de 2 vecteurs ne saurait se réduire à la connaissance de ses coordonnées dans une base, même si on a pris le soin de préciser qu'elle doit être orthonormée et directe.
-
La matrice d'un endomorphisme auto-adjoint n'est symétrique que si elle le représente dans une base orthonormée. Même remarque pour la matrice d'un automorphisme orthogonal.
-
Lors de la résolution de certains problèmes d'algèbre linéaire, on peut être amené à résoudre des équations ou des systèmes différentiels linéaires. Il est exigé des candidats qu'ils le fassent avec la même rigueur que lors de l'épreuve de Math I. En particulier, il n'est pas autorisé de diviser par
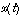 sans justifier qu'une solution non identiquement nulle ne s'annule jamais sur son intervalle de définition, ni de remplacer
sans justifier qu'une solution non identiquement nulle ne s'annule jamais sur son intervalle de définition, ni de remplacer 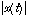 par
par 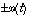 .
.
-
Le calcul de la distance d'un vecteur à un sous-espace de dimension finie doit pouvoir être mené à bien, et le logiciel de calcul formel peut alors se montrer efficace !
Espérant que la lecture de ces lignes aidera les futurs candidats et leurs professeurs à la préparation de l'épreuve, nous tenons à féliciter les quelques très bons candidats que nous avons pu interroger. Les qualités dont ils ont fait preuve leur seront utiles tant dans la poursuite de leurs études que dans l'exercice de leur futur métier d'ingénieur.
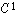 par morceaux ?
par morceaux ?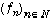 vers f suffit pour montrer que
vers f suffit pour montrer que 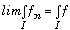 quand I est un intervalle quelconque.
quand I est un intervalle quelconque.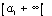 et l'existence de
et l'existence de 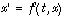 et pour les systèmes autonomes ne sont pas connus.
et pour les systèmes autonomes ne sont pas connus.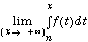
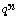 tend vers zéro, dès lors que
tend vers zéro, dès lors que 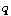 est inférieur à 1.
est inférieur à 1.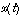 sans justifier qu'une solution non identiquement nulle ne s'annule jamais sur son intervalle de définition, ni de remplacer
sans justifier qu'une solution non identiquement nulle ne s'annule jamais sur son intervalle de définition, ni de remplacer 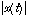 par
par 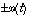 .
.