Mathématiques I
Le niveau d'ensemble des candidats de la filière MP, dans cette épreuve d'oral de Mathématiques I, a été tout aussi satisfaisant que celui de l'année dernière. L'esprit des nouveaux programmes apparaît même mieux perçu et, au niveau du comportement individuel, les candidats, dans leur grande majorité, essaient visiblement de faire de leur mieux lors de leur prestation orale.
Les recommandations d'ordre général figurant en préambule dans le rapport de l'épreuve d'oral de Mathématiques I de 1997 semblent avoir été prises en considération. Elles demeurent évidemment valables pour le concours à venir c'est pourquoi, tout en rappelant ci-dessous les intitulés des divers paragraphes, il est conseillé aux futurs candidats de s'y reporter.
- Réfléchir à l'énoncé proposé et ne pas se contenter d'une lecture superficielle du texte.
- Être attentif à la rigueur de l'exposé que l'on va présenter.
- Savoir initier un dialogue avec l'examinateur lorsque la résolution de l'exercice semble bloquée : un oral n'est pas une épreuve écrite au tableau.
- Annoncer à l'examinateur les méthodes que l'on compte utiliser.
- Savoir faire, en cours d'épreuve, le bilan des questions résolues.
On y ajoutera une recommandation d'ordre pratique, celle d'arriver en salle d'attente quelques minutes avant l'heure de convocation au lieu d'être juste à l'heure ou légèrement en retard, ce qui risque d'induire une difficulté à se concentrer en début d'épreuve.
Les conseils visant à une amélioration de la compréhension du nouveau programme d'analyse concernent essentiellement l'usage des théorèmes puissants admis sur la convergence dominée et les intégrales dépendant d'un paramètre.
Un théorème ne se résume pas à l'énoncé d'une formule, il n'est pas une recette à appliquer sans avoir préalablement réfléchi aux hypothèses de son application.
Un autre conseil d'ordre général est de comprendre l'utilité, dans certaines situations, de faire un usage rigoureux des quantificateurs. Dans ce cas, toute lettre doit être précédée d'un quantificateur. Cela contribuerait à éviter l'utilisation d'expressions, certes imagées mais sans réel contenu mathématique, du genre "faisons tendre maintenant 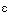 vers 0" et cela aiderait, par ailleurs, à nier correctement une phrase mathématique.
vers 0" et cela aiderait, par ailleurs, à nier correctement une phrase mathématique.
Dans le même ordre d'idées, un examen soigné des premiers termes est utile pour rechercher une formule de récurrence.
Rappelons avec insistance que les théorèmes suivants, parmi d'autres, sont hors programme et ne sauraient donc être pris en compte dans l'évaluation du candidat :
- théorème général de sommation par paquets pour les familles sommables ;
- transformation d'Abel ;
- règle de Cauchy
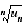 ou règle de Raabe-Duhamel ;
ou règle de Raabe-Duhamel ;- théorème de la convergence radiale pour les séries entières ;
- théorème de Fubini pour des intégrales doubles définies sur des intervalles non compacts.
En revanche, des résultats au programme restent mal connus d'un trop grand nombre de candidats. Ainsi la fonction 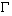 n'est que rarement reconnue lorsqu'elle apparaît au détour d'une question et des lacunes importantes apparaissent au niveau des formes différentielles (lien entre formes exactes et formes fermées, simple dessin d'un ouvert étoilé dans le plan).
n'est que rarement reconnue lorsqu'elle apparaît au détour d'une question et des lacunes importantes apparaissent au niveau des formes différentielles (lien entre formes exactes et formes fermées, simple dessin d'un ouvert étoilé dans le plan).
De même, les résultats concernant les séries 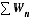 avec
avec
et f fonction positive décroissante et continue par morceaux, ou f de classe 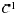 à valeurs complexes et telle que f' soit intégrable sur
à valeurs complexes et telle que f' soit intégrable sur 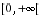 , apparaissent totalement ignorés des candidats.
, apparaissent totalement ignorés des candidats.
La liste suivante d'erreurs ou maladresses les plus fréquemment commises n'est pas exhaustive.
Espaces vectoriels normés et suites d'éléments
Condition nécessaire et suffisante d'égalité dans l'inégalité de Minkowski méconnue.
La distance de deux fermés disjoints peut être nulle.
La distance d'un point à un ensemble 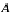 est nulle si et seulement si ce point appartient à
est nulle si et seulement si ce point appartient à 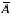 .
.
La propriété 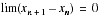 n'entraîne pas la convergence de la suite
n'entraîne pas la convergence de la suite 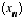 .
.
Caractérisation des fermés par les suites souvent mal citée.
Réticence à utiliser la caractérisation séquentielle de la continuité.
Une application bilinéaire non nulle et continue n'est pas lipschitzienne.
Il faut réfléchir à ce que peut être une fonction équivalente à la fonction nulle.
Séries d'éléments d'un espace normé
Borner les sommes partielles d'une série ne prouve pas que la série converge.
En cas d'éclatement du terme général d'une série en termes de séries divergentes, penser aux sommes partielles.
Penser à étudier la suite 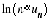 pour déterminer la nature d'une série
pour déterminer la nature d'une série 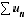 à termes strictement positifs.
à termes strictement positifs.
Ne pas abuser de la règle de d'Alembert alors que l'étude de la valeur absolue du terme général 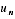 permet souvent de conclure par simple majoration. Elle est bien sûr sans intérêt pour étudier la nature d'une série entière aux bornes de son intervalle de convergence. Si on l'utilise, ne pas oublier les valeurs absolues et ne pas diviser par 0.
permet souvent de conclure par simple majoration. Elle est bien sûr sans intérêt pour étudier la nature d'une série entière aux bornes de son intervalle de convergence. Si on l'utilise, ne pas oublier les valeurs absolues et ne pas diviser par 0.
N'utiliser le théorème sur les séries alternées qu'après avoir vérifié que l'on ne peut conclure par convergence absolue et, si on l'utilise, ne pas croire que la décroissance d'une suite se transfère par équivalence.
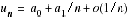 ne se traduit pas par
ne se traduit pas par 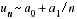 . Attention, de même, au passage à l'équivalence avec la fonction exponentielle, ou à l'addition d'équivalents.
. Attention, de même, au passage à l'équivalence avec la fonction exponentielle, ou à l'addition d'équivalents.
Les résultats sur les séries de Bertrand doivent pouvoir être rapidement justifiés, puisqu'ils sont a priori non exigibles.
Séries doubles de nombres réels ou complexes
Les hypothèses concernant l'interversion des 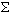 sont mal connues.
sont mal connues.
Suites et séries de fonctions, séries entières, séries de Fourier
Le théorème de Weierstrass n'est pas celui de Stone-Weierstrass.
Réticence à essayer d'utiliser la convergence normale.
La convergence uniforme locale est utile pour établir continuité et dérivabilité de la somme.
Les développements en série entière classiques sont souvent ignorés.
Le théorème de la projection orthogonale d'un vecteur x d'un espace préhilbertien réel E sur un sous-espace vectoriel F de dimension finie est mal cité.
Trop de candidats ignorent que
ne dépend pas de x lorsque la fonction f est T-périodique et continue.
Les primitives d'une fonction continue périodique ne sont en général pas périodiques.
Dérivation et intégration
Les formules locales (Taylor-Young ou développements limités) sont inopérantes pour l'obtention des encadrements globaux.
Attention au changement de variable dans le cas d'une fonction f qui n'est que continue par morceaux sur un intervalle I.
Une somme de Riemann n'est pas la somme partielle d'une série.
Lorsque la fonction f est à valeurs complexes, on ne dispose que d'une inégalité de Taylor-Lagrange.
La formule de Taylor avec reste intégral est souvent fausse.
Dans le vaste champ des questions relatives à l'intégrabilité sur un intervalle non compact, plusieurs observations sont à faire.
- La vérification de l'intégrabilité est souvent faite sans soin. On se contente d'une étude aux bornes sans autre précision sur les propriétés de la fonction entre ces bornes.
- La continuité par morceaux est souvent oubliée. Certains candidats en arrivent ainsi à conclure à l'existence de
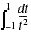 .
.- La définition des intégrales impropres est bien au programme même si aucune connaissance spécifique sur les intégrales semi-convergentes n'est exigible des candidats.
- Pour les intégrales à paramètre, il est indispensable de bien préciser les intervalles de la variable d'intégration et du paramètre afin d'appliquer correctement les théorèmes de continuité et de dérivabilité sous le signe somme.
- Beaucoup de candidats s'obstinent à chercher des majorations uniformes sur tout le domaine alors que des majorations uniformes sur un compact quelconque inclus dans ce domaine sont suffisantes (même remarque que pour les suites et séries de fonctions).
- La convergence uniforme sur un intervalle non borné ne suffit pas pour pouvoir effectuer une intégration terme à terme.
indépendante de X n'assure pas l'intégrabilité de f.
Équations différentielles
La méthode de la variation des constantes pour les équations différentielles linéaires du second ordre reste mal appliquée par un candidat sur deux.
Fonctions de plusieurs variables réelles
La continuité des applications partielles n'entraîne pas la continuité.
Les calculs de dérivées partielles sont en général mal conduits, les symétries de la fonction sont rarement utilisées.
Une utilisation maladroite des relations de domination ou d'équivalence quand il y a des paramètres conduit souvent à masquer un problème de double limite.
Géométrie différentielle
L'aire d'un triangle peut intervenir au cours d'une question.
Les constructions de courbes en coordonnées paramétriques ou polaires posent des problèmes aux candidats. Ainsi, pour les courbes en coordonnés polaires.
- Les branches infinies du type
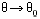 et
et 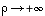 sont presque systématiquement mal étudiées (on a pour asymptote la droite d'équation
sont presque systématiquement mal étudiées (on a pour asymptote la droite d'équation 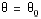 ).
).L'équipe des examinateurs de l'épreuve de Mathématiques I souhaite que ce rapport puisse servir aux futurs candidats ainsi qu'à leurs professeurs. Ils sont convaincus qu'ils tireront profit tout au long de leur carrière professionnelle future du travail en profondeur qu'ils effectuent pendant leurs années de préparation au concours.
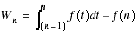
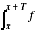
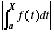
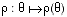 est souvent préférable à celle de son tableau de variations.
est souvent préférable à celle de son tableau de variations.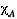 pour le polynôme caractéristique d'une matrice
pour le polynôme caractéristique d'une matrice 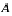 , ce qui est bien encore si l'on est bon calligraphe au cas où les lettres
, ce qui est bien encore si l'on est bon calligraphe au cas où les lettres 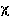 et
et 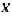 se jouxtent... L'examinateur d'un candidat hyperdécontracté entendit parler, non sans stupeur, de la méthode du
GOSSE
(méthode de Gauss) pour déterminer la signature d'une forme quadratique ! Ajoutons que la définition intrinsèque est toujours utile, comme par exemple pour une forme quadratique définie sur
se jouxtent... L'examinateur d'un candidat hyperdécontracté entendit parler, non sans stupeur, de la méthode du
GOSSE
(méthode de Gauss) pour déterminer la signature d'une forme quadratique ! Ajoutons que la définition intrinsèque est toujours utile, comme par exemple pour une forme quadratique définie sur 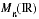 et non pas
et non pas 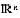 .
.