Mathématiques I
L'objet du
problème
est l'étude d'une famille de fonctions à valeurs complexes et l'établissement de la formule des compléments en utilisant la transformation de Laplace.
Rares sont les candidats qui énoncent correctement et complétement les théorèmes utilisés : il ne suffit pas de dire "d'après le théorème de convergence dominée, on obtient le résultat demandé".
Tous les correcteurs ont noté une détérioration de la situation par rapport aux années précédentes au niveau de la logique et de la rigueur: la question I.A a montré que la définition même de 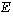 n'était pas toujours comprise et que beaucoup confondaient non vide et non réduit à zéro. La notion d'inclusion entre deux ensembles est souvent erronée; on a vu beaucoup d'implications du genre :
n'était pas toujours comprise et que beaucoup confondaient non vide et non réduit à zéro. La notion d'inclusion entre deux ensembles est souvent erronée; on a vu beaucoup d'implications du genre : 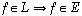 donc
donc 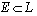 .
.
La différence entre condition nécessaire et condition suffisante n'est que très rarement perçue : la réponse à la question III.A3b commence très souvent par "pour que 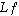 possède une limite en zéro, il faut que...".
possède une limite en zéro, il faut que...".
Les questions de majoration ont aussi suscité beaucoup d'erreurs, de nombreux candidats semblant ignorer que la relation d'ordre sur les réels ne se prolonge pas aux complexes.
Partie I
I.A) L'expression "stable par" n'est pas comprise par certains.
I.B) Cette question a donné lieu à beaucoup de fautes de logique.
I.C) Plus de la moitié des candidats ne sait pas comment aborder le problème de l'intégrabilité de 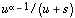 sur I. La notion même d'intégrabilité n'est pas comprise : l'utilisation du terme intégrale convergente a nui aux candidats. Beaucoup ne comprennent pas le sens de la seconde partie de la question : ils oublient de montrer que le coefficient de proportionnalité qu'ils obtiennent est indépendant de s.
sur I. La notion même d'intégrabilité n'est pas comprise : l'utilisation du terme intégrale convergente a nui aux candidats. Beaucoup ne comprennent pas le sens de la seconde partie de la question : ils oublient de montrer que le coefficient de proportionnalité qu'ils obtiennent est indépendant de s.
Partie II
II.A) Il est demandé d'être précis dans l'énoncé du théorème, de ne pas parler de continuité sans préciser par rapport à quelle(s) variable(s) et sur quel(s) ensemble(s).
II.B1) Beaucoup ont compris qu'ils devaient utiliser le théorème de convergence dominée mais très peu l'ont fait convenablement, en particulier très peu donnent la bonne domination.
II.B2) La notion d'équivalent n'est pas assimilée.
II.B3 et C) Ces questions, difficiles, n'ont été résolues que dans les meilleures copies.
Partie III
III.A1) Certains candidats pensent qu'une fonction continue sur I est nécessairement bornée. Les comparaisons entre 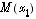 et
et 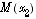 ont souvent donné lieu à des discussions vaseuses.
ont souvent donné lieu à des discussions vaseuses.
III.A2) Le lien avec la question précédente n'a pas toujours été vu et l'oubli du module de f a été fatal à beaucoup.
III.A3a) Cette question, identique à II.A, a donné lieu aux mêmes erreurs.
III.A3b) Dans les exemples de fonctions donnés, beaucoup ne sont pas dans 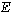 .
.
III.B1) Contrairement à ce que pensent certains candidats, la fonction 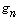 n'est pas la restriction de
n'est pas la restriction de 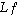 à l'intervalle
à l'intervalle 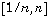 . Concernant la convergence de la suite de fonctions
. Concernant la convergence de la suite de fonctions 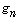 vers
vers 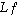 , une justification était attendue.
, une justification était attendue.
III.B2) Là encore, pour appliquer le théorème de Fubini, il fallait énoncer avec précision les hypothèses. La justification du passage à la limite est rarement donnée.
III.B3) C'est là une question difficile, résolue seulement dans les bonnes copies.
III.B4) Très peu de candidats ont compris le sens de la question.
III.B5) Question, rarement bien traitée, qui n'était qu'une utilisation des résultats obtenus auparavant.
Partie IV
IV.A) Très peu de candidats vérifient que la fonction est bien définie ; la présence de valeurs complexes perturbe les majorations.
IV.B) Rarement résolue.
IV.C) Quelques "filous" concluent un calcul qui tournait mal par une égalité abrupte. Le changement de variable est souvent bien fait. Bien que le problème soit long, certains candidats gardent assez de lucidité pour utiliser les calculs précédents et trouver la valeur de l'intégrale de Gauss.
Mathématiques II
Le
problème
demandait de démontrer d'abord quelques propriétés élémentaires des matrices orthogonales, symétriques positives et antisymétriques, ceci en dimension 2 et relativement au produit scalaire usuel sur 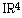 . Puis il introduisait à l'étude des quaternions réels et à la paramétrisation associée de
. Puis il introduisait à l'étude des quaternions réels et à la paramétrisation associée de 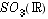 .
.
La partie du programme concernée, algèbre linéaire essentiellement, est plus familière aux étudiants que la géométrie, c'est là une différence importante avec les années précédentes. Cela s'est traduit surtout par un allongement notable des copies, même quand celles-ci étaient de mauvaise qualité. Nous reviendrons plus loin sur les lacunes de fond les plus fréquentes, mais on peut d'ores et déjà renouveler une mise en garde faite depuis de nombreuses années. Les candidats doivent présenter des raisonnements et des résultats
clairs
. Sur ce point, il est certain que les candidats peuvent améliorer grandement leurs copies par un simple effort de concision. N'hésitons pas à affirmer que les candidats ne sont pas ici jugés sur leur rapidité d'écriture... et qu'une copie sur trois est deux fois trop longue. Cet effort profiterait d'abord au candidat qui aura ainsi mis en valeur des raisonnements justes sans les enfouir au milieu d'un véritable brouillon, et qui saura un peu mieux lui-même où il en est.
Concision et clarté, voilà un effort de communication qui devrait être naturel à de futurs ingénieurs.
La perte de temps engendrée pour les candidats qui passent autant de temps à broder sur les questions faciles les empêche souvent d'aborder les questions plus importantes.
Cette concision devrait d'abord s'exercer comme une censure des affirmations hasardeuses voire malhonnêtes, auxquelles le candidat lui-même n'accorde aucun crédit : calculs faux ou interrompus à la moitié, mais conclus par un péremptoire "d'où le résultat demandé", arguments empruntés à un cours imaginaire comme «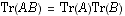 ». Nous ne nous permettrions pas cette mise en garde si la bonne foi des candidats n'était prise en défaut dans des proportions inquiétantes (un quart des copies comporte ce type de défaut).
». Nous ne nous permettrions pas cette mise en garde si la bonne foi des candidats n'était prise en défaut dans des proportions inquiétantes (un quart des copies comporte ce type de défaut).
Il est clair que le correcteur assimilera toujours à un blanc ce type de remplissage, imputable peut-être à une culture commerciale (?) très mal assimilée.
Comme on le voit, nos conseils portent plus sur la manière de composer et sur l'esprit que requiert un écrit de mathématiques, que sur tel ou tel point du programme. Voici ci-dessous quelques remarques sur les difficultés de l'énoncé et les lacunes apparentes des candidats.
I.A.1) Une moitié des candidats s'avère incapable de fournir une matrice 4x4. On relève également beaucoup d'erreurs de signes dans les matrices.
I.A.2) Des preuves très longues. Certaines "montrent" 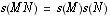 .
.
I.B) L'argument selon lequel N serait le noyau d'une forme linéaire, donc un hyperplan, ne se rencontre que trop rarement.
II.A.1) Ici comme en III.A.4. il faut vérifier qu'une forme à deux variables est un produit scalaire. Beaucoup de démonstrations sont incomplètes, et ce n'est pas incompatible, trop longues. Il y a essentiellement quatre points assez indépendants à vérifier. La considération de 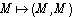 ne suffit pas.
ne suffit pas.
II.B) En utilisant la base définie par 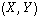 , il est facile de voir que
, il est facile de voir que 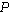 est la symétrie orthogonale par rapport à
est la symétrie orthogonale par rapport à 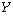 , et que
, et que 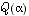 est la rotation d'angle
est la rotation d'angle 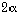 . Notons que les deux composantes connexes de
. Notons que les deux composantes connexes de 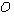 ,
, 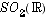 et son complémentaire, sont des cercles de rayon
et son complémentaire, sont des cercles de rayon 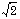 sur les plans en somme directe orthogonale
sur les plans en somme directe orthogonale 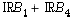 et
et 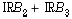 .
.
II.B.2) Cette question a été interprétée dans un cinquième des copies comme demandant de montrer 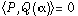 , ce qui a parfois été correctement montré.
, ce qui a parfois été correctement montré.
II.C) Les démonstrations correctes, même dans l'idée générale, sont rarissimes.
II.E.1) Une généralité : on oublie souvent de montrer que le résultat obtenu est dans l'ensemble voulu. En II.E.1 que 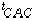 (resp. B) est symétrique, en IV.A.1 que
(resp. B) est symétrique, en IV.A.1 que 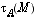 est dans
est dans 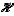 .
.
Notons que cette partie II peut être démontrée en toute dimension. Elle se réduit d'ailleurs au cas de la dimension 2.
III) La proportion de cette partie traitée par le candidat a largement déterminé son rang pour cette épreuve. C'est pourquoi nous avons insisté sur la gestion du temps et la concision des copies : il est clair que les candidats qui se sont rassurés en noircissant 6 copies doubles sur les parties I et II n'ont pas eu le temps de faire grand chose de la partie III.
III.A.I) On a trop souvent vu l'argument selon lequel "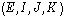 est libre donc une base puisque
est libre donc une base puisque 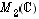 est de dimension 4"... oubliant qu'à ce compte-là on aurait
est de dimension 4"... oubliant qu'à ce compte-là on aurait 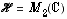 !
!
Par contre, l'égalité
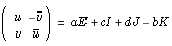
lorsque 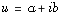 et
et 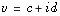 pour a, b, c, d réels, avec unicité, permettait de vérifier à la fois que
pour a, b, c, d réels, avec unicité, permettait de vérifier à la fois que 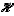 est un
est un 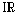 -espace vectoriel et que
-espace vectoriel et que 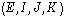 en est une base.
en est une base.
III.B) Il est très rare de voir comme argument que 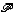 est le noyau d'une forme linéaire non nulle.
est le noyau d'une forme linéaire non nulle.
III.C.2) Ce calcul a souvent été conduit convenablement. Par la suite, l'idée de ce changement de variable et des endomorphismes ainsi construits en dimension 3 n'a été comprise que par très peu de candidats, mais parfois brillamment.
Nous concluons sur cette note encourageante.
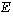 n'était pas toujours comprise et que beaucoup confondaient non vide et non réduit à zéro. La notion d'inclusion entre deux ensembles est souvent erronée; on a vu beaucoup d'implications du genre :
n'était pas toujours comprise et que beaucoup confondaient non vide et non réduit à zéro. La notion d'inclusion entre deux ensembles est souvent erronée; on a vu beaucoup d'implications du genre : 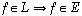 donc
donc 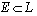 .
.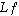 possède une limite en zéro, il faut que...".
possède une limite en zéro, il faut que...".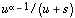 sur I. La notion même d'intégrabilité n'est pas comprise : l'utilisation du terme intégrale convergente a nui aux candidats. Beaucoup ne comprennent pas le sens de la seconde partie de la question : ils oublient de montrer que le coefficient de proportionnalité qu'ils obtiennent est indépendant de s.
sur I. La notion même d'intégrabilité n'est pas comprise : l'utilisation du terme intégrale convergente a nui aux candidats. Beaucoup ne comprennent pas le sens de la seconde partie de la question : ils oublient de montrer que le coefficient de proportionnalité qu'ils obtiennent est indépendant de s.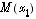 et
et 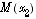 ont souvent donné lieu à des discussions vaseuses.
ont souvent donné lieu à des discussions vaseuses.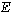 .
.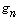 n'est pas la restriction de
n'est pas la restriction de 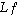 à l'intervalle
à l'intervalle 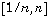 . Concernant la convergence de la suite de fonctions
. Concernant la convergence de la suite de fonctions 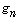 vers
vers 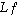 , une justification était attendue.
, une justification était attendue.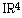 . Puis il introduisait à l'étude des quaternions réels et à la paramétrisation associée de
. Puis il introduisait à l'étude des quaternions réels et à la paramétrisation associée de 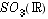 .
.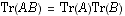 ». Nous ne nous permettrions pas cette mise en garde si la bonne foi des candidats n'était prise en défaut dans des proportions inquiétantes (un quart des copies comporte ce type de défaut).
». Nous ne nous permettrions pas cette mise en garde si la bonne foi des candidats n'était prise en défaut dans des proportions inquiétantes (un quart des copies comporte ce type de défaut). 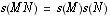 .
.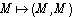 ne suffit pas.
ne suffit pas. 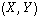 , il est facile de voir que
, il est facile de voir que 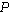 est la symétrie orthogonale par rapport à
est la symétrie orthogonale par rapport à 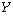 , et que
, et que 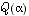 est la rotation d'angle
est la rotation d'angle 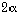 . Notons que les deux composantes connexes de
. Notons que les deux composantes connexes de 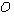 ,
, 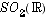 et son complémentaire, sont des cercles de rayon
et son complémentaire, sont des cercles de rayon 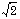 sur les plans en somme directe orthogonale
sur les plans en somme directe orthogonale 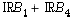 et
et 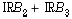 .
.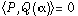 , ce qui a parfois été correctement montré.
, ce qui a parfois été correctement montré.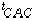 (resp. B) est symétrique, en IV.A.1 que
(resp. B) est symétrique, en IV.A.1 que 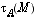 est dans
est dans 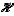 .
.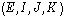 est libre donc une base puisque
est libre donc une base puisque 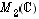 est de dimension 4"... oubliant qu'à ce compte-là on aurait
est de dimension 4"... oubliant qu'à ce compte-là on aurait 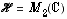 !
!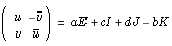
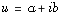 et
et 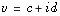 pour a, b, c, d réels, avec unicité, permettait de vérifier à la fois que
pour a, b, c, d réels, avec unicité, permettait de vérifier à la fois que 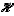 est un
est un 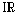 -espace vectoriel et que
-espace vectoriel et que 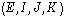 en est une base.
en est une base.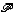 est le noyau d'une forme linéaire non nulle.
est le noyau d'une forme linéaire non nulle.